Maximum internal volume isn't the same thing as maximum utility, but consider this simplified 2D case anyway:
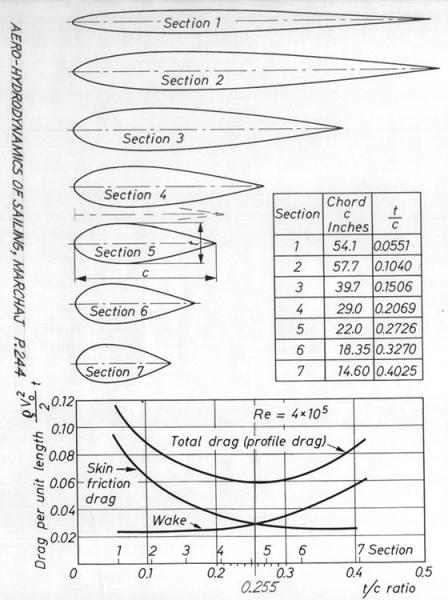
Give each car the same length "c=1". Each of these sections has the same packing factor, so internal area is proportional to "t" alone. So, in the above plot, you want to maximize the value of the x-axis divided by the y-axis. It's gonna be really long and skinny.
But maybe you can do better by taking section 5, slicing it at its widest point, and extending it with flat sides in the middle?
Buses, trailers, and oil tankers are vehicles with large ratios of internal volume to aerodynamic drag.
Also, a vehicle can improve its ratio of volume to drag simply by being scaled up.