Quote:
Originally Posted by RobertSmalls

Maximum internal volume isn't the same thing as maximum utility, but consider this simplified 2D case anyway:
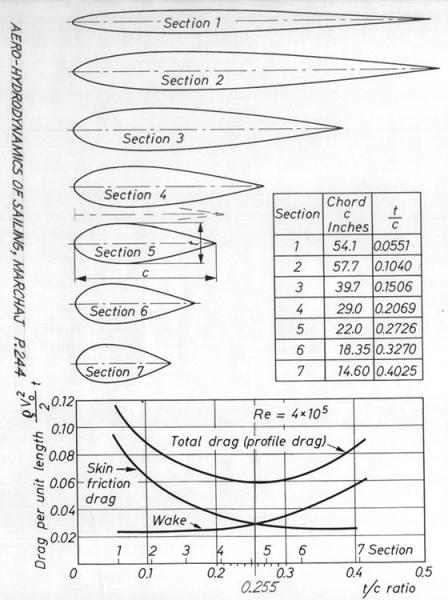
Give each car the same length "c=1". Each of these sections has the same packing factor, so internal area is proportional to "t" alone. So, in the above plot, you want to maximize the value of the x-axis divided by the y-axis. It's gonna be really long and skinny. |
I'm not sure I follow your reasoning on this. Section 7 will have more internal volume than Section 5 for the same length.
Section 7 is 0.4025/0.2726 = 1.47 times as thick as Section 5.
Looking at the drag curves, Section 5 has a Cd of about .06 and Section 7 has a Cd of about .086. .086/.06 = 1.43, so Section 7 has only 1.43 times the drag, but 1.47 times the thickness.
Also, I think the greater curvature of the thicker section will include a proportionately larger area (volume if 3d) than the maximum thickness numbers would suggest.