[bwilson4web]

Originally Posted by redpoint5

So far I'm disappointed at what Google has to say on the subject. From Wiki:

"A high compression ratio is desirable because it allows an engine to extract more mechanical energy from a given mass of air-fuel mixture due to its higher thermal efficiency."

In other words, a high compression ratio is more efficient because it is more efficient.

From answers.com:

"Engine efficiency is increased though compression ratio by allowing a more thermodynamic energy to be converted into mechanical energy. Energy transfer is the key to efficiency."
. . .

I'm sorry, I should have been more specific. So let's start with this URL:

Internal combustion engine - Wikipedia, the free encyclopedia

They don't really discuss compression ratio but this is the take away:

. . .
The thermodynamic limits assume that the engine is operating in ideal conditions: a frictionless world, ideal gases, perfect insulators, and operation at infinite time. The real world is substantially more complex and all the complexities reduce the efficiency. In addition, real engines run best at specific loads and rates as described by their power band. For example, a car cruising on a highway is usually operating significantly below its ideal load, because the engine is designed for the higher loads desired for rapid acceleration. The applications of engines are used as contributed drag on the total system reducing overall efficiency, such as wind resistance designs for vehicles. These and many other losses result in an engine's real-world fuel economy that is usually measured in the units of miles per gallon (or fuel consumption in liters per 100 kilometers) for automobiles. The miles in miles per gallon represents a meaningful amount of work and the volume of hydrocarbon implies a standard energy content.

Most steel engines have a thermodynamic limit of 37%. Even when aided with turbochargers and stock efficiency aids, most engines retain an average efficiency of about 18%-20% . . . .

Practical, commonly sold engines have abysmal thermal dynamic efficiencies. To be perfectly blunt, they are rubbish compared to what they could (and should) achieve.

So lets switch to two university web pages that go into details addressing the effect of compression ratio:

3.5 The Internal combustion engine (Otto Cycle)
Design of an Otto Cycle

Both papers show the math to derive the same efficiency formula for a 'perfect' Otto cycle engine:

efficiency = 1 - ( 1 / (r ** (k-1) ) )

r - compression ratio
k - specific heat ratio, a measure of energy in the fuel

For simplicity, here is the MIT chart:


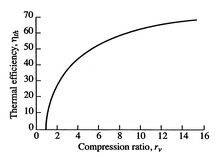
Here is the Northwestern chart:

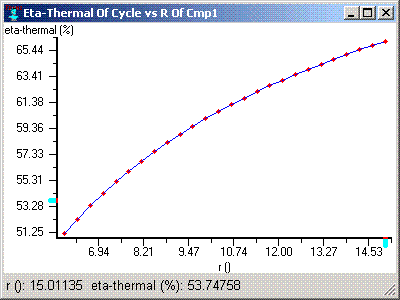
Note they have have different scales with the MIT showing the full range and the Northwestern a more practical range we find today.

Now everything in these classical, Otto cycle lessons derives from the P-v diagram:


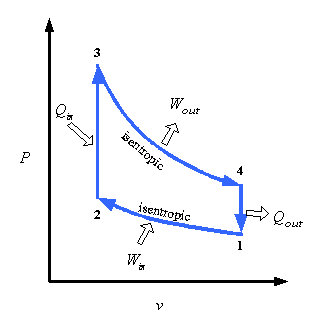
The top curve coming from point 3 towards point 4 is the power stroke curve and the longer it is, the more energy extracted. The x-axis is the "v" expansion ratio.

Bob Wilson

ps. I don't know if you are interested but the Prius Atkinson cycle takes the line from 1 to 2 and breaks it into two sections:

1 to 1.5 - this is a flat line as the intake valve is kept open and part of fuel-air mix goes back into the intake manifold to be sucked in the next cylinder.

1.5 to 2 - this is the shortened compression stroke which being smaller, means less compression losses.

Qs - the energy added is less because there is less fuel-air to burn

Qout - is the same

4 - is moved to the right about 50% further (aka., 13 to 1 expansion versus 9 to 1 typical compression ratio.) So the Prius has a much longer power stroke to extract more energy.

I do not like this P-v chart but it is 'close enough:'

I do not like it because the segment 3-4 implies a substantial increase in volume without work being done and that doesn't happen. If you stretch 4 over to combine it with 3, you'll have an accurate, Atkinson cycle P-v diagram.

Bob Wilson