Quote:
Originally Posted by Astro

Does this sound correct?
Assuming a 50% duty cycle square wave and a battery (Vs) voltage of say 20V and a current of 100A.
SW1 closed
Battery Volts = 20V
Inductor Volts = 20V
Capacitor Volts = 40V
Battery Amps = 100A
Inductor Amps = 100A
Capacitor Amps = 0A
SW1 open
Battery Volts = 20V
Inductor Volts = 20V
Capacitor Volts = 40V
Battery Amps = 100A
Inductor Amps = 100A
Capacitor Amps = 100A
So the capacitor is supplied double the battery voltage for half the time at battery current.
D1 is there to prevent the capacitor being shorted when SW1 closes.
The battery delivers a constant 100A at 20V.
The inductor charges and discharges to 20V at 100A.
As long as the load placed on the capacitor discharges at an average current of half the battery current or less then the capacitor will supply twice the battery voltage.
|
Yes.
The capacitor is initially charged to 20V, rather than 40, by the diode. This is where the pre-charge goes. From here the boost converter charges the output capacitor in pulse by pulse current limiting, which also means that if the output is too large it will simply throttle back the output voltage.
I like to say that the battery current is twice the output current for half the duty cycle, which is about the same and its also valid for the switch, inductor, diode and output capacitor, which can now supply the nominal output, but your principle is correct.
Technically since this is done at HF the value averages, and its the reason a capacitor is needed at the input of the converter, to average the battery current.
For continuous mode, the minimum inductor current is the output current (200A) and the maximum current is the output added to the ripple. So the smaller the ripple the smaller the current with minimum being the load current.
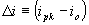
From this the interesting thing is the RMS current
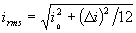
For an output of 200Amps and a 30% ripple, the RMS value comes as 60Amps, again backing up my last post that only the ripple current contributes toward the losses.
Here's the link:
Boost Switching Converter Design Equations
The formulas to calculate the inductor current in function of the inductance are also there.