I finally got around to some images which may help to visualize the concept of our vehicle's effective fineness ratio.
*From Hucho,we see that the vehicle is resolved into itself,plus it's mirror image.It's effective fineness ratio includes the vehicles length,divided by the height of the vehicle PLUS it's mirror companion.

*From the higher Reynolds number curve it's evident that the drag minimum occurs when the effective fineness ratio is 2.5:1.
*Ellipsoids and streamline bodies of revolution share identical drag coefficients for identical fineness ratios.Here is a drag table for streamline bodies in free flight.
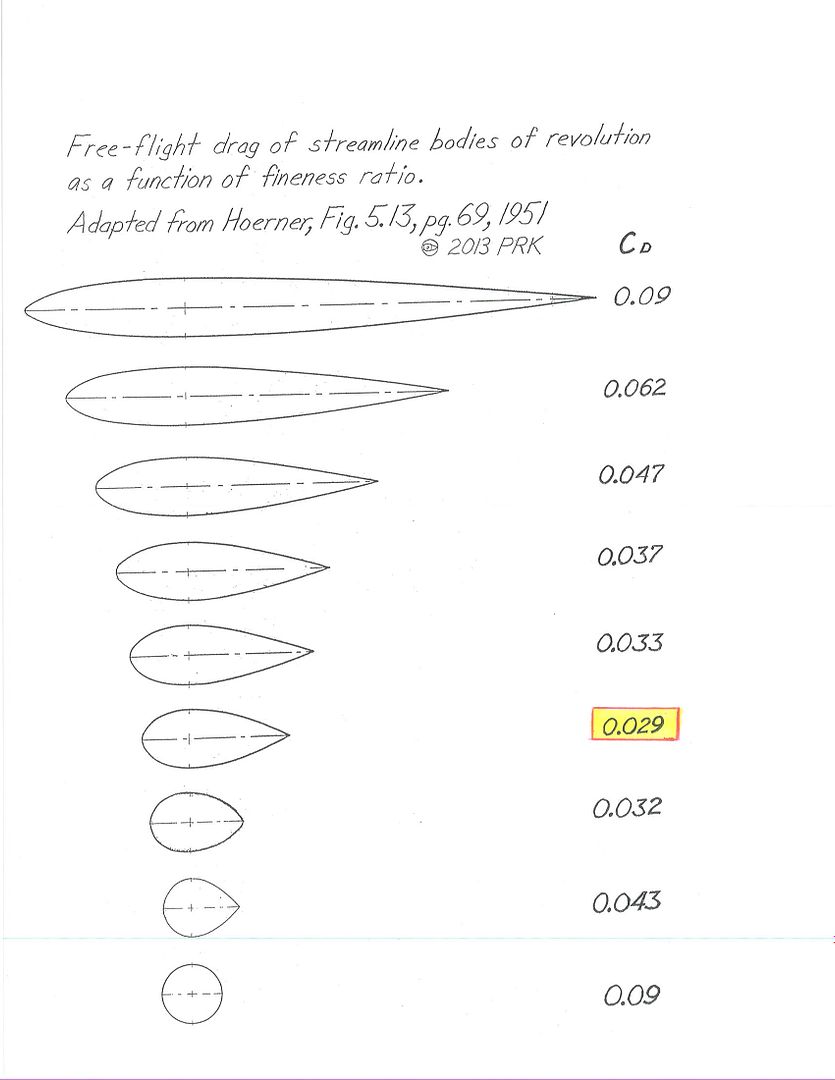
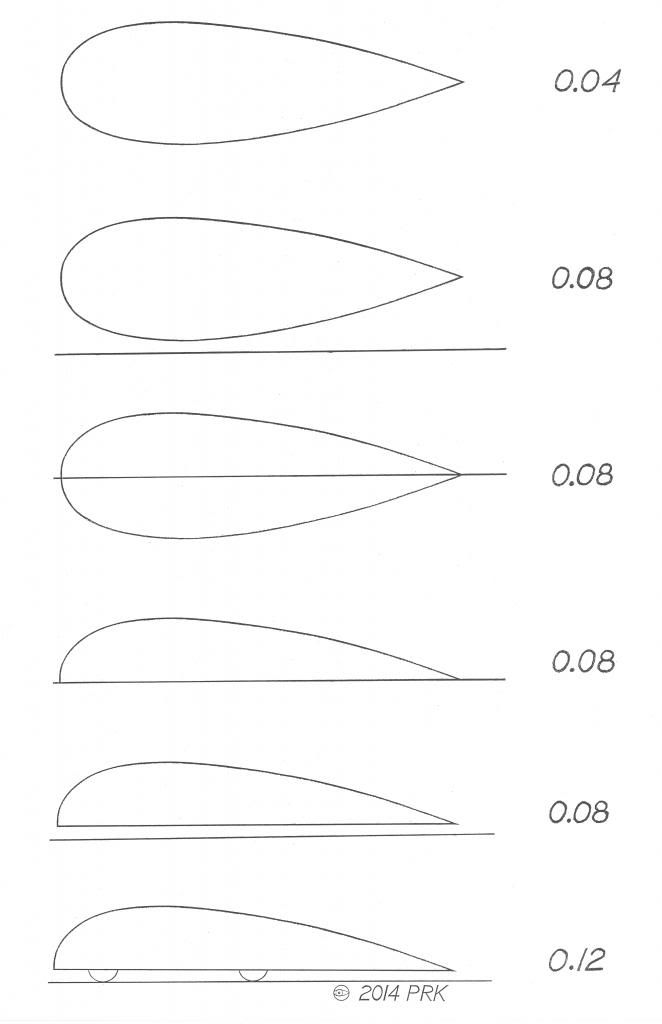
*The 2.5:1 body has the drag minimum.NOTE: these are not frontal area-based Cds.But you see that the numerical minimum occurs with 2.5:1.
*For a frontal area-based coefficient of aerodynamic drag for this body in free flight you'll find Cd 0.04.
*As the body moves into ground proximity it's drag doubles.
*A 'half-body' possesses this 'doubled' drag,or Cd 0.08.
*Adding skinny wheels.tires brings drag up to Cd 0.12.
--------------------------------------------------------------------------
Here is a 3-car montage of Hucho's Beetle,plus one of Kamm's K-cars,and Walter Lay's Model# 22 in ground reflection.

*At each 'leap' in Effective fineness,the car gets it's drag cut about in half.
*Here,I've superimposed a rough outline of Jaray's ideal contour
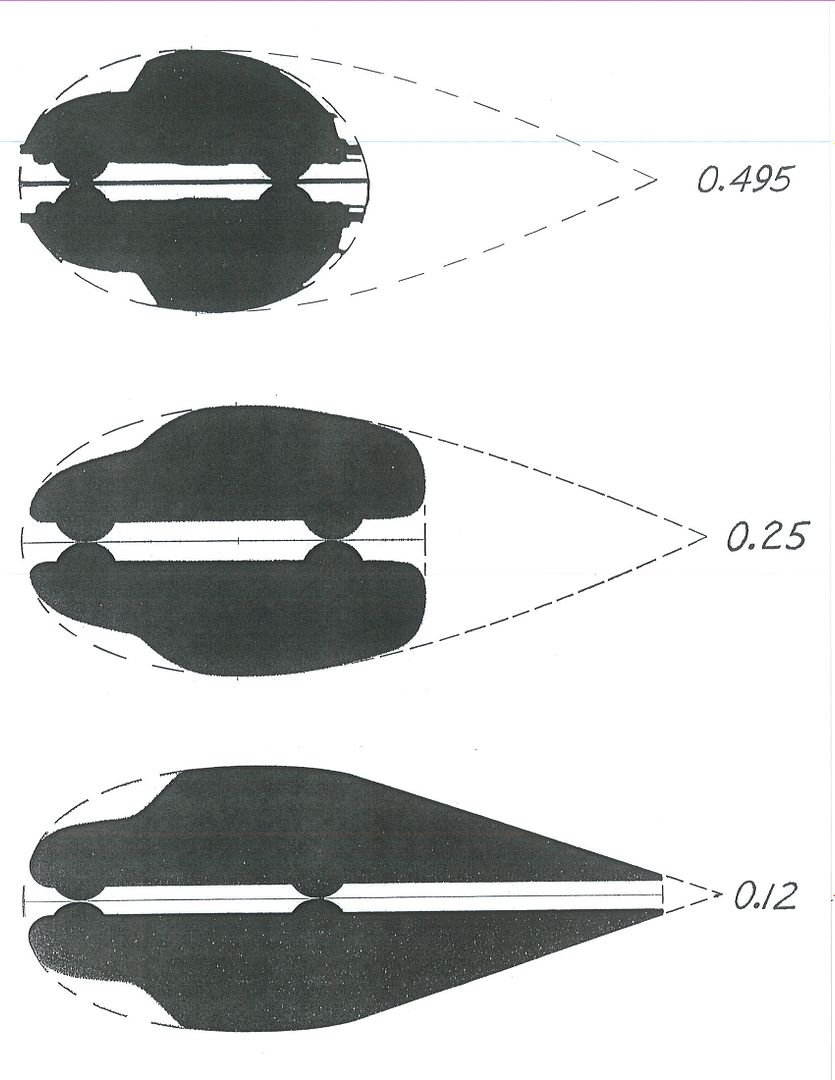
*As the 'void' is filled in under the 'Template' the drag reduces by means of wake reduction.We can't eliminate it altogether due to the half-ring of turbulent boundary layer sloughing off the tail of the car,but it's enough to get us to Cd 0.12,plus mirrors,features drag,and cooling system.
*With wheel fairings you're looking at Cd 0.10,to 0.08.
------------------------------------------------------------------------
*So when you're considering Hucho's 'elongation' for drag reduction,bear in mind that you've got to deal with 'both' your cars.