The BSFC chart thread (post 'em if you got 'em)

[roflwaffle]

Originally Posted by cfg83

roflwaffle -

At around 1100 RPM in 5th gear, I would see as high as 91 LOD. But it wouldn't stay there. As the RPMs ever-so-slowly increased with the MPH, it would fall off. I will do the test again at 1500 RPM, but now I am leaning toward assuming that that it's measuring torque.

CarloSW2

There's no way it's measuring power if you see 91/100 at ~1100rpm/5th. I found an interesting description of LOD as the percent of power (probably meant torque) requested, so I wonder if your load is falling off due to a decrease in VE (volumetric efficiency) w/ speed...

[TestDrive]

Originally Posted by OldGuy

Here is a link to an article which is very helpful in understanding BSFC charts:

Browser Warning

Enjoy.

Thanks, OldGuy. I thought that AutoSpeed.com article link was one of the most useful and informative links in the whole thread.

Given that vehicle specific BSFC maps can be difficult (if not impossible) to find, perhaps the Averaged* BSFC Maps found in the article have some relevance.
...* Includes V8, V6 & 4-cyl engines.

diagrams are sourced from a 1999 report prepared for the Canadian government by Sierra Research of California. The diagrams are based on a sample of 1995 model year, naturally aspirated, EFI 2-valve engines

...

Here each dot shows the speed and load for a typical mid size car at 1 second intervals during the US fuel economy test. Of the time the car takes to do the test, just 5 seconds are in the island of best BSFC. Quite a few of the dots (the authors say that they overlay) are at worst BSFC – idling at zero load with the car stationary!

Not sure that it's all that meaningful - but for purpose of comparison - here is scale-matched** overlay on the Saturn 1.9L Map including Doax's plot of HP/rpm from his Matrix.
...** The vertical scale is probably incorrect. The Average map's vertical scale is BMEP but I don't know how that relates to newton meters. I took BMEP for ft/lbs and scaled accordingly.

[cfg83]

TestDrive -

Vair-eeeee eeeen-tay-rest-ink. I wonder if this averaged BSFC map is a strategy being used inside the ScanGauge.

CarloSW2

[tasdrouille]

Might be a dumb question, but what is a Graham scanner?

[Wonderboy]

Certainly couldn't find any graphs on my D16Y8 (98 Civic EX), but I did come across a wealth of raw data for Toyota folks.

Enjoy

Gasoline engines

It was linked to from this discussion:
Let's talk BSFC... - onecamonly.com

[some_other_dave]

Originally Posted by TestDrive

The Average map's vertical scale is BMEP but I don't know how that relates to newton meters.

My understanding is quite incomplete, but I believe that the two are related, but not identical. BMEP is "Brake Mean Effective Pressure", I think, and is a measurement of the pressures inside the cylinder. More cylinder pressure typically means more torque from a given motor under a given set of operating conditions, but I think there are a bunch of other factors that also have some sort of influence on the one figure or the other.

So a direct scale overlay is probably "close enough" for our purposes, even though it may be technically inaccurate.

-soD

[TestDrive]

Originally Posted by some_other_dave

My understanding is quite incomplete, but I believe that the two are related, but not identical. BMEP is "Brake Mean Effective Pressure", I think, and is a measurement of the pressures inside the cylinder. More cylinder pressure typically means more torque from a given motor under a given set of operating conditions, but I think there are a bunch of other factors that also have some sort of influence on the one figure or the other.

So a direct scale overlay is probably "close enough" for our purposes, even though it may be technically inaccurate.

-soD

Some_other_dave, that's my same basic understanding of BMEP.

When I created the overlay, I figured it was "close enough" to be useful, but felt it was probably well short of "best guess, reasonable approximation." After looking at it a while longer, I decided a Saturn 1.9L would probably have fewer city driving cycle samples in the sweet spot (????), so I scaled vertical down by and additional 10%.


Revised aspect of Generic BSFC map using BMEP = 150.8 x TORQUE (lb-ft) / DISPLACEMENT (ci) as a guide to matching BMEP and Torque scales of the Generic and Saturn maps.

Also made various changes to attempt to improve visual clarity including:

• Improved contrast.
• Where applicable changed SFC labels to reflect both SI and US units of measure.
• SFC labels from the Generic Map are now in italics
• SFC labels from the Saturn Map are now in bold
• SFC labels on both maps now appear above and to the left of the lines they reference.

[TestDrive]

Back on page 4 of this thread, sickpuppy318 posted a BSFC Map with overlaid blue lines of constant horsepower.
Earlier today while looking for info on how to relate BMEP to Nm or ft.lb (guess I'll be revising the overlay), I came across the same Map in a TDIClub forum. The post that introduce the map had this to say -

A more useful illustration is to superimpose curves of constant power onto a BSFC map.

Each curve represents a constant horsepower developed by the engine. If you are driving on a given road with a constant grade, speed, and ambient conditions (TestDrive's emphasis), regardless of which gear you are in, it requires roughly the same amount of power to overcome aerodynamic drag, rolling resistance and driveline losses. Therefore, regardless of what gear you're in, you're riding anywhere along the same blue curve; exactly where you sit on that blue curve being only dependent on the gear you're in and therefore the RPM at which the engine is turning over.

If I take the example of operating on a certain speed such that the power is 20 HP, The lowest BSFC occurs when running at the gear that corresponds to about 1250 RPM. If I run at either a higher- or lower RPM from this point, my BSFC will increase. This is about the only point in the entire engine map where it would be disadvantageous to operate at an even higher gear if one were available (lower RPM) because of the worsening BSFC. Almost everywhere else, the lowest BSFC is achieved at the lowest possible RPM at a given power.

[Deezler]

Originally Posted by TestDrive

info on how to relate BMEP to Nm or ft.lb (guess I'll be revising the overlay), I came across the same Map in a TDIClub forum. The post that introduce the map had this to say -

Good find, that post on TDIclub is some good reading on the subject.

Thanks to all that have posted in this thread too, interesting discussion. And I really appreciate finding the BSFC map for my engine! As soon as I saw it I knew I had to start experimenting in excel. Unfortunately, not having the data meant re-creating it. Didn't take long though: Pretty close, I'd say.

from:


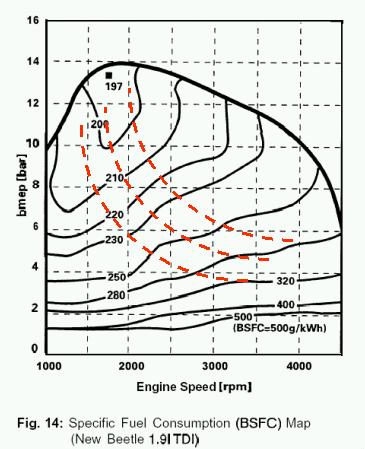
to:


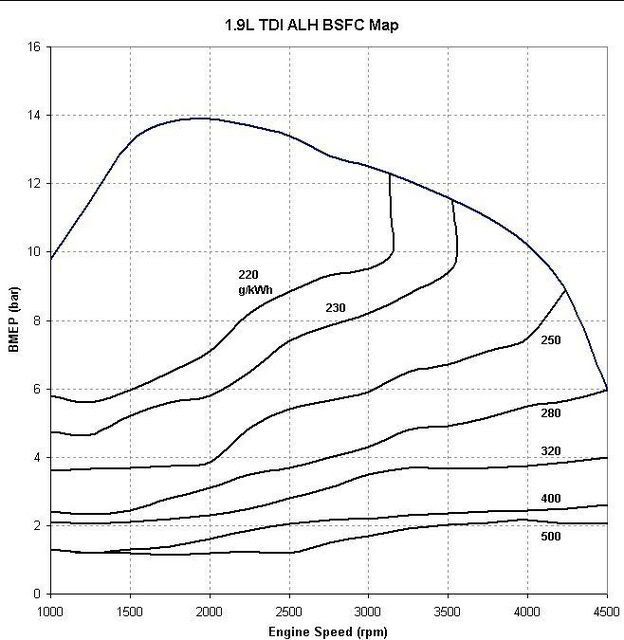
For some background: BMEP (brake mean effective pressure) is directly comparable to torque, regardless of engine speed. I wont try to type formulas here, but you basically just relate torque to the mean pressure acting downwards on the piston times displacement and divided by 4*pi.
With units of bar (= 100 kPa), the result is torque in N-m (newton-meters).
BMEP is most often simply calculated from the brake torque as measured on an engine dynamometer. It becomes very useful when you measure the actual cylinder pressure with a transducer, calculate the indicated mean effective pressure (IMEP), and subtract the BMEP to obtain the FMEP, or friction losses of the engine due to rubbing, rotating, accessory drives, and pumping losses.

Now that we have a decently accurate BSFC map set of data, we can overlay other data for comparison. For example, the lines of constant power in blue on the 2nd version of this plot. While those are neat for reference, they aren't especially practical, since you cant just adjust your rpm while driving down the road to maximize efficiency. (of course gearing changes do this though - more on that later).

I decided to look at the power requirements due to real road loads when traveling in top gear (where I do most of my driving). I was going to calculate a bunch of stuff when I found the aerodynamic and rolling resistance HP loss calculator on this site, very handy!
Aerodynamic & rolling resistance, power & MPG calculator - EcoModder.com

My input data:
VW Jetta Mk4
weight = 3300 lbs
Cd = 0.30
Crr = 0.010
Area = 21.8 ft^2
Fuel = B20 biodiesel
Air Density = 1.293 kg/m^3 (0 C)

very cool. Copied the data out and pasted into excel. Now we have the aerodynamic and rolling losses calculated from 5 to 120 mph.
Next, I calculated the engine rpm in top gear when traveling through that same speed range with my tire size and gear ratio #s. If we assume we're stuck in 5th gear, we can overlay a plot of the aero and rolling load on the vehicle vs engine rpm. The calculated HP loss is converted to torque through rpm. Vehicle speed is on the top axis for reference.



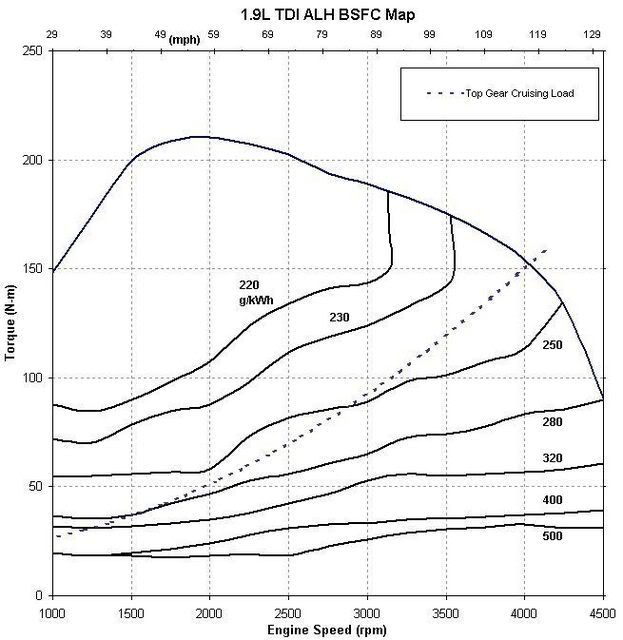
But what if we can lower our aerodynamic drag? My goal for my jetta is to get down to Cd = 0.27. Probably optimistic given how good it is to start with. We'll see (mirror delete and other tricks on the way this spring).

Re-calculating, we can compare.



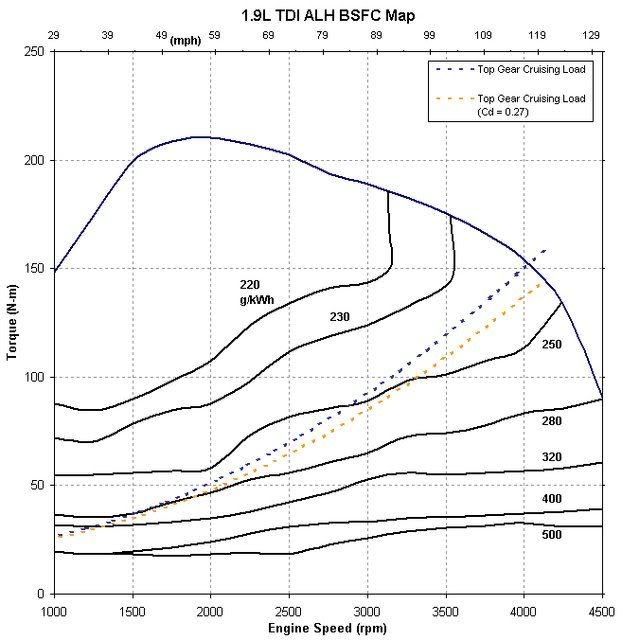
So you can see that reducing our road load with the same vehicle gearing, we are actually moving the engine operation into a less efficient area. Bad thing? No way! because even though the efficiency has declined for the same vehicle speed, we are requesting less load and our overall fuel consumption has still declined. I ran a comparison calculation:

Traveling at 2500rpm = 72.5 mph
I fit 2nd order polynomials to the aero and rolling calculation lines (R^2 = 1). Back calculating real road load at this speed, converting to power @ 2500rpm, and interpolating between BSFC lines to estimate the specific fuel consumption, we generate the following data:

2500 rpm = 72.5 mph
Cd Nm kW BSFC est g/hr L/h gal/h mpg
0.30 69.21 18.11 263 4762.91 5.60 1.48 48.98
0.27 64.48 16.87 269 4538.95 5.34 1.41 51.39

Pretty darn cool, especially since the calculated fuel consumption matches what I record in driving nearly perfectly (the 49 mpg, that is). So we can now calculate directly the effect that a given aero improvement will have upon mileage! nice. Interpolating between the BSFC lines is a little bit of a guesstimation, but its the best we can do.

Next up: Gearing reductions through a swapped out 5th gear or tire size changes! I'll try to post up these comparisons on Monday. hint: the road load lines move to the left.

[some_other_dave]

Wow, Deez, thanks! Looks like I was confusing IMEP and BMEP in my post; it's really good to have someone with more knowledge of what is actually going on posting here!!

-soD