Coastdown Test 06 GMC Canyon

[JRMichler]

I finally got an opportunity to do a coastdown test of my Canyon. Flat roads don't seem to exist in Northern Wisconsin, but I finally found one in Central Wisconsin. A stretch of Highway 73 located a few miles west of Plainfield is flat to less than five feet and was lightly traveled on that day.

Elevation 1060 feet, temperature 17 deg F, wind 5 to 7 MPH from the SE. That particular stretch of road ran NW. Tires at 48 PSI, estimated gross weight with gas, luggage, and people was 4650 lbs.

My brother sat in the back seat and aimed a video camera at the speedometer. Data reduction consisted of watching the video and recording the time at which the speedo needle passed 60, 57.5, 55, etc MPH. The data was entered into a spreadsheet.

Ran the test once in each direction, so had a direct tailwind and a direct headwind. The following image shows the speed vs time for the two runs.

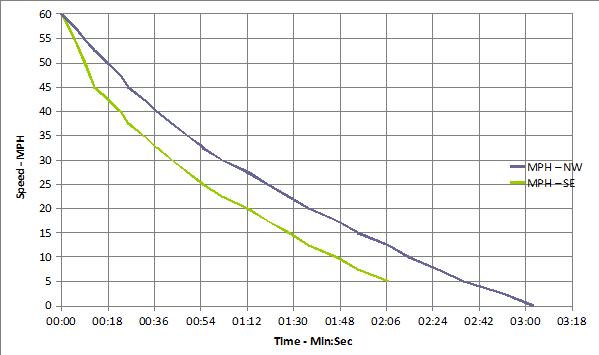
The wind speed was only 5 to 7 MPH according to wunderground.com and barely noticeable according to personal observation, but that was enough to significantly affect the two coastdown runs. I stopped the second coastdown before getting to a full stop because of traffic.

The rate of deceleration is the change in speed (2.5 MPH) divided by the time for that speed change. With the speed converted to Ft/Sec, the result came out in Ft/Sec^2. Dividing the deceleration by 32.2 and multiplying by the total weight (4650 lbs) gives the total drag force at that speed.

The following two images show the drag vs speed for the two runs along with the best fit equation. The first image is with the tailwind, the second image with the headwind. Note that how much effect an extremely light breeze has on the total drag. A 5 to 7 MPH wind feels almost like a dead calm.




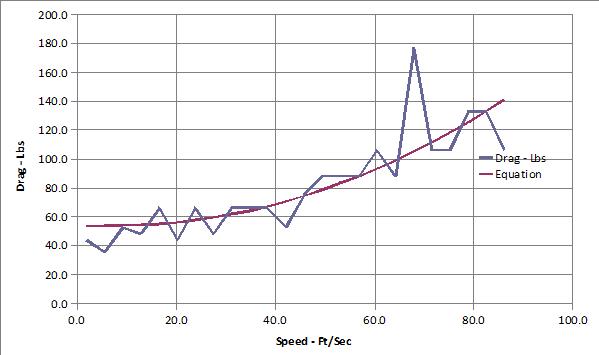
An equation of the form:
Drag = (Airspeed)^2 + Rolling Resistance was fit to both sets of data using least squares. The airspeed was actual speed minus windspeed in one direction and actual speed plus windspeed in the other direction. Windspeed was a parameter and part of the least squares process.

The result was this equation: Drag = 0.0143 X Airspeed^2 + 0.0116 X Mass. Since the total mass was 4650 lbs, the equation can also be shown as: Drag = 0.0143 X Airspeed^2 + 54 lbs.

This approach implies that the total rolling friction (Crr plus wheel bearings plus brake drag plus differential gears plus driveshaft friction plus transmission friction) is 0.0116 times the total weight of the truck.

The CdA can be calculated from this equation. Pick an arbitrary speed, say 100 ft/sec. The aero drag is 0.0143 X 100^2 = 143 lbs. The air density at 17 deg F at 1060 feet elevation is 12.4 lbs/ft^3, so the velocity pressure at 100 ft/sec is 0.5 X 0.0806 lbs/ft^3 / 32.2 X 100^2 = 12.52 lbs/ft^2. The CdA is then 143 / 12.52 = 11.4 ft^2.

The frontal area is estimated to be 67.6" X 65.2" X 0.84 / 144 = 25.7 ft^2. The Cd is estimated to be 11.4 / 25.7 = 0.44.

I suspect that much of the bearing and driveline drag is proportional to speed. If so, adding a linear term to the regression equation would increase overall accuracy. Doing that would require a better data set - start from a higher speed and both runs need to go to a full stop.

[JRMichler]

OK, now let's calculate what MPG I should get at a steady 55 MPH.

55 MPH = 80.7 Ft/Sec.
Drag = 0.0143 X 80.7^2 + 54 = 147 lbs.
Hp = 147 Lbs X 80.7 Ft/Sec / 550 Ft-Lbs/Hp = 21.6 Hp.
Estimated fuel consumption = 21.6 X 0.5 Lbs / Hp-Hr / 6 Lbs/Gallon = 1.8 GPH.
Estimated MPG = 55 MPH / 1.8 GPH = 30.6 MPG.

This is almost exactly what I would expect on a 17 degree day with zero wind at 55 MPH. Now, I had a good turbodiesel at 0.35 lbs / Hp-Hr, I would expect 43.7 MPG under the same conditions. DROOL.

[Sven7]

That's some serious math there... went right over my head. Would you be down for doing some calculations for a confused art student?

Assuming I can get out and get some data! It's great to get an estimated CdA!

[JRMichler]

No problem, I can help walk you through it. If you want to do a coastdown test, your best approach is to just get started and save the calculation stuff for later.

Find a straight level stretch of road and coast both ways with a video camera on the speedometer. Use one of the free online topo map sites to find a level road. Look for 5 foot contours with no contour lines crossing the stretch of road that you will be using. Then look at the road - it should look absolutely level.

Try for zero wind. Second best is a very light breeze straight down the center of the road. Crosswinds are very bad - they act like a headwind both ways. It's a good idea to run a garbage test to work out how to do the test.

The regression equation from my test showed a 5.5 MPH wind. That light a wind almost feels like a dead calm, but you can see from the first graph just how much it affected the test.