Aerodynamic Streamlining Template: Part-C

[some_other_dave]

Note that the curvature of a number of the mathematically-generated teardrop shapes is concave. I don't believe that's what we want, so that should place a limit on the "m".

Actually, it looks like the curvature may be convex at some point (close to the tail) for almost any value of m. Fortunately we don't usually take the boat-tail all the way to a point, so that's not a worry for us.

-soD

[sgtlethargic]

Thanks for making me feel better, guys.

[sgtlethargic]

Here are the AST-II and the teardrop graph (m = 1) overlaid using Merge. Pretty close. I think the AST front end is blunted.

[freebeard]

That's OK.

If you extend this idea any more yourself, you should consider a dedicated thread.

Like aerohead sez, this deprecates all previous Templates through mathematical rigor.

Here's the picture I did, that popped up in a thread I was reading:


This guy PRK is just all over the place.

[aerohead]

I'm starting a thread-within-a-thread as the images to follow are all germane to the 'Template.'
It will take some time to get them all completed and posted,so please bear with me.
--------------------------------------------------------------------------
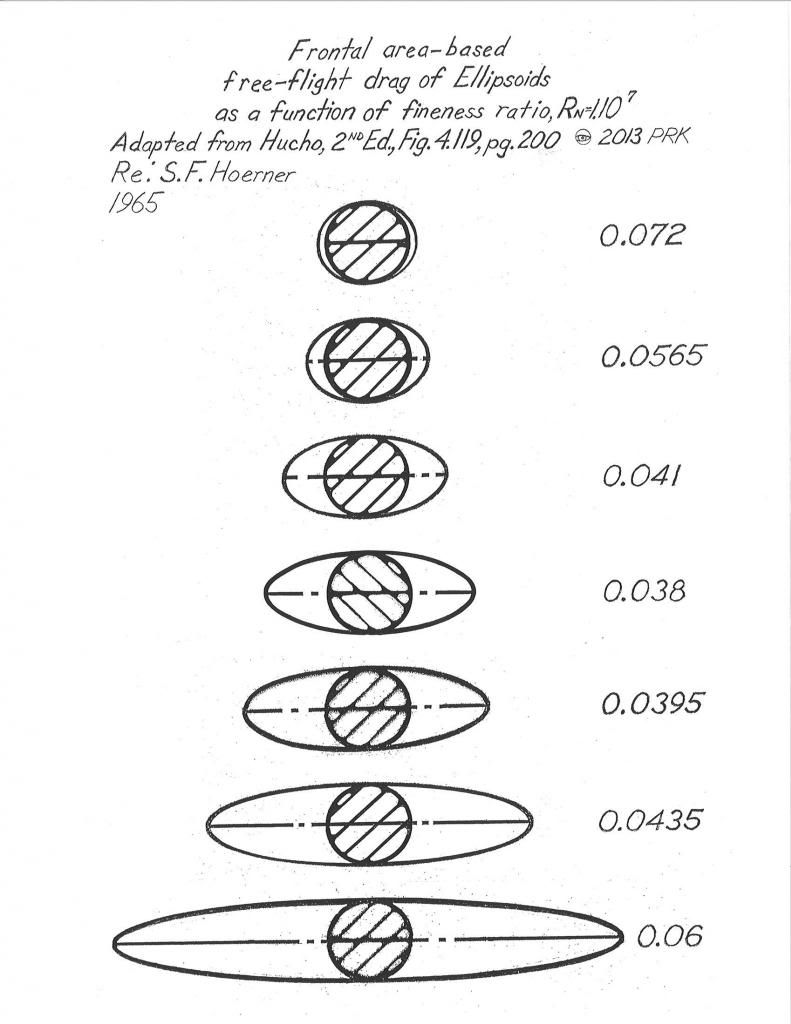
I'm starting with what I feel is the most significant,the streamline bodies of revolution which in ground proximity,as 'half-bodies,show the highest potential as low drag forms.
They are all 'teardrops',and as you see from the table,their drag varies as a function of fineness-ratio,with highest drag matched,top and bottom;where the top is overwhelmed with surface skin friction,and bottom is overwhelmed by pressure drag.
The data was originally presented as a drag curve plot of frontal area Cd vs L/D.
The images are actually borrowed from 'section' profiles presented by C.J.Marchaj (of which he credits Sighard Hoerner for the quanta) and are not to be taken as 'templates',but only to illustrate the relationship of L/D to overall drag.
-------------------------------------------------------------------------
From the research of Jaray,Prandtl,and Rumpler,any of these bodies would see 'double' the drag in close ground proximity,and in mirror-image ground reflection.
------------------------------------------------------------------------
The lowest Cd is associated with L/D= 2.1,although as a half-body in mirror-image,this body would violate boat tail tangent angles found to support attached boundary layer flow of 'bluff bodies' without artificial,power-induced stimulation.
Attached flow is absolutely essential to low drag.
An L/D=2.5 appears to be the minimum architecture which satisfies the requirement for complete attached flow and is the model for the Aerodynamic Streamlining Template.A 'teardrop' near the L/D= 2.5 appears fourth from the bottom of the table.
-------------------------------------------------------------------------
All the 'templates' to be presented will have a 'sweet spot',just as with wing sections and struts,where the curves for surface skin friction and pressure drag cross to create the drag minimum.These 'minimums' are what we're most interested in.
------------------------------------------------------------------------
'Teardrops'

--------------------------------------------------------------------------
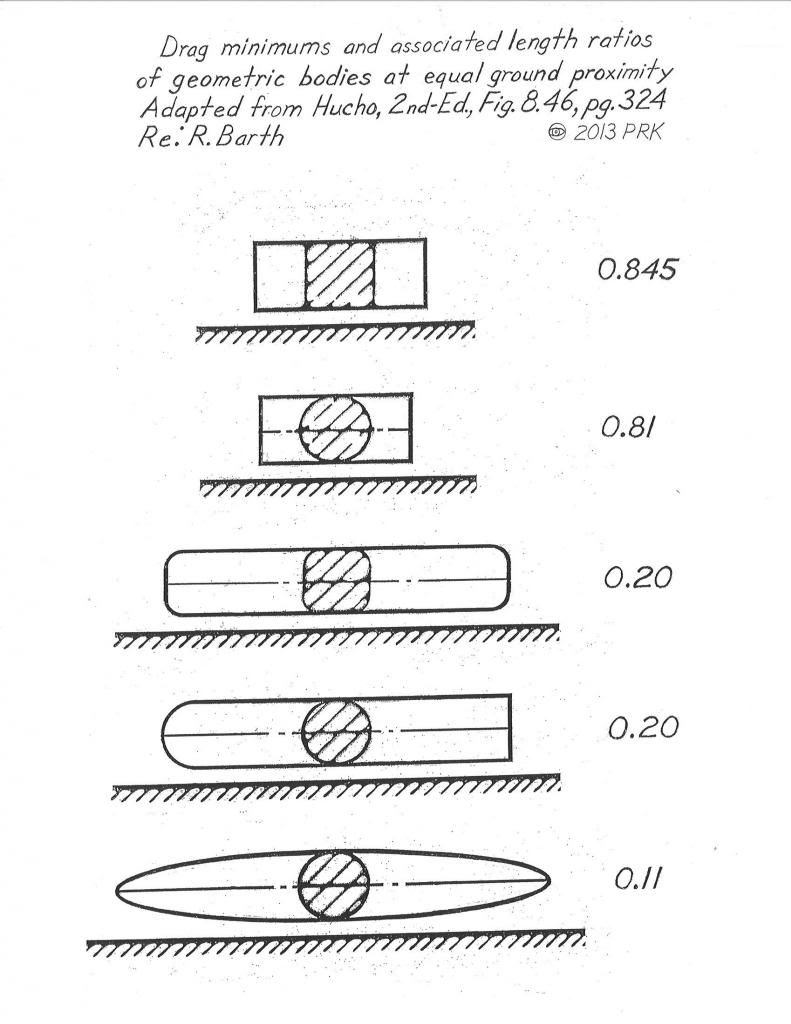
Here are some ellipsoids of differing drag and also some assorted geometric bodies which were tested at the same ground clearance.The latter are presented at the fineness ratio of minimum drag,or,'sweet spots,'according to the research of R.Barth.

[California98Civic]

Thanks! Subscribed.

[3-Wheeler]

Originally Posted by sgtlethargic

Why are there no comments on the Excel graphs?

After digging around for a mathematical solution to the posted equation by Mathematica, I came across a description of what is meant by "sin^m" listed above.

The math form below shows another way of handing the "sin^m", which is not solvable by normal means.



So now we had a way of properly solving the shape of a Tear Drop, and an excerpt is shown below. Here are the equations for X and Y:

X=COS(A10)
Y=SIN(A10)*SIN((A10/2)^$F$8)/$C$7

Where:
Increment = 0.1 (number of desired steps in shape)
A10 = cell A10
$C$7 = 1.925 (constant) used to create a shape with a 2.5:1 length/width ratio
$F$8 = M (constant)

And here is what the spreadsheet data looks like....



To solve for a shape where Y is positive, vary T from 0 to PI. To solve for a shape where Y is negative, vary T from PI to 2PI. In this case I am only interested in solving for Y in the positive state, so T is varied from 0 to PI.

Here is the original graph presented by SGT.

I'm not sure about the Y-axis units for this graph, as they do not give output of 2.5:1 for length/width.



The graph below however does indeed maintain AeroHead's 2.5:1 length/width ratio however. We have "two units" in the X-axis (-1 to +1) and one-half of the 0.8 units of width (0.4 units) shown. 2.0/0.8 = 2.5:1



SGT, thanks for posting your original graph of this shape, as it gave me the incentive to dig deeper for those who are math challenged, like myself.

Hope this helps, Jim.

[betasniper]

Did this in about 2 hours. Straightened the Original template in solidworks, Made a spline, Exported spline into Paint.net, Texted, Angle Tested (off by about .5° on a couple angles), Done.

[KamperBob]

One peeve with Excel is I cannot find an option to force 1:1 aspect ratio between X and Y axes. (pout)

[freebeard]

My problem is that in my head, Y is up-down and Z is nominally front-to-back. So I'm not sure I'm interpreting all this correctly. T=Z?

Anyway, the reason I'm bumping the thread is this YouTube video. It appears to show an unnamed Excel-SketchUp interface. There's no audio [in this browser in this location] and if I search on 'DST Manager' or 'Domain Specific Tool Manager' I hit dead ends.

http://www.youtube.com/watch?v=KPMyWt8Rvps