Aerodynamic Streamlining Template: Part-C

[Tesla]

Hey all,
Been away for a few years, but recently got inspired to dig out the old spreadsheets and have another play with the equations and after a lot of fiddling I finally managed to get the specs down pat.
2.5:1 Aspect ratio
1.78:Tail ratio
And also managed to get the kink out of the tail, I have left the x & y grid visible and they are in the same graduations so one can easily measure the grid lines on screen (zoom for more detail) to ensure x:y proportional integrity, i.e. the squares should be true squares.
Here is the calculated curve:



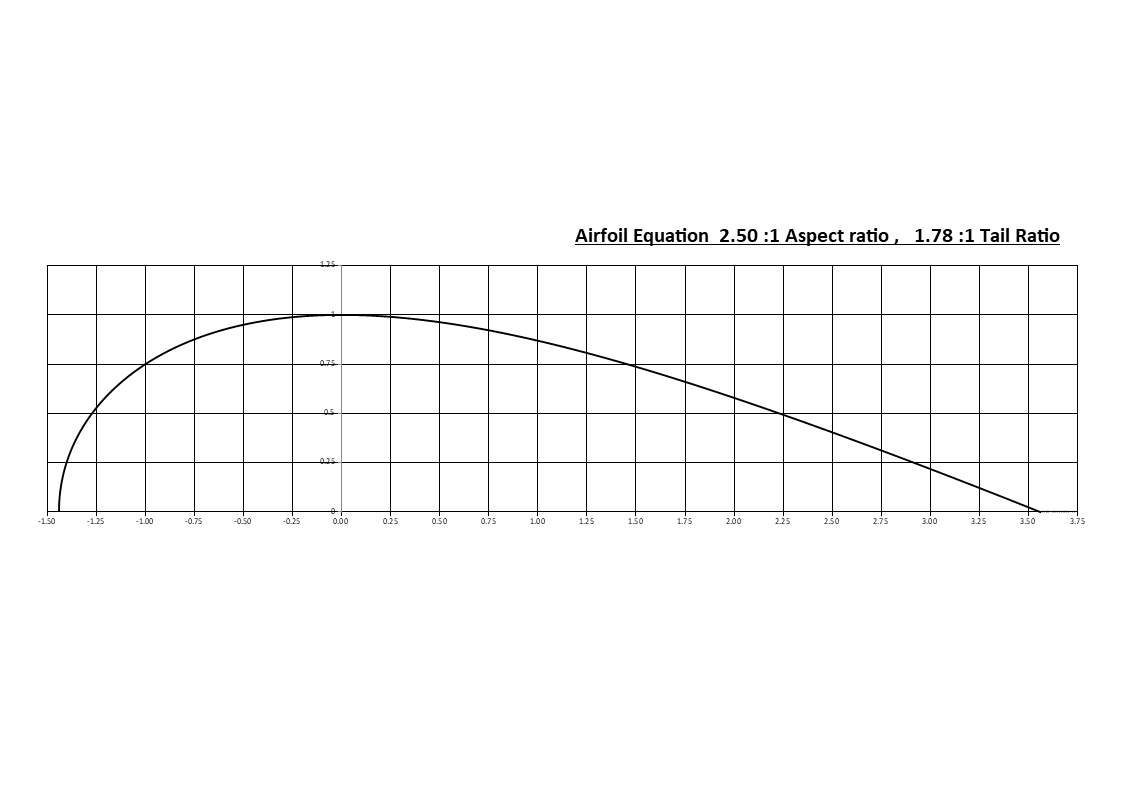
The next stage was to overlay the Template AS-II, which is just slightly more aggressive than the specified ratios, both the 2.5 and the 1.78 which the equation is limited to, overlay below:



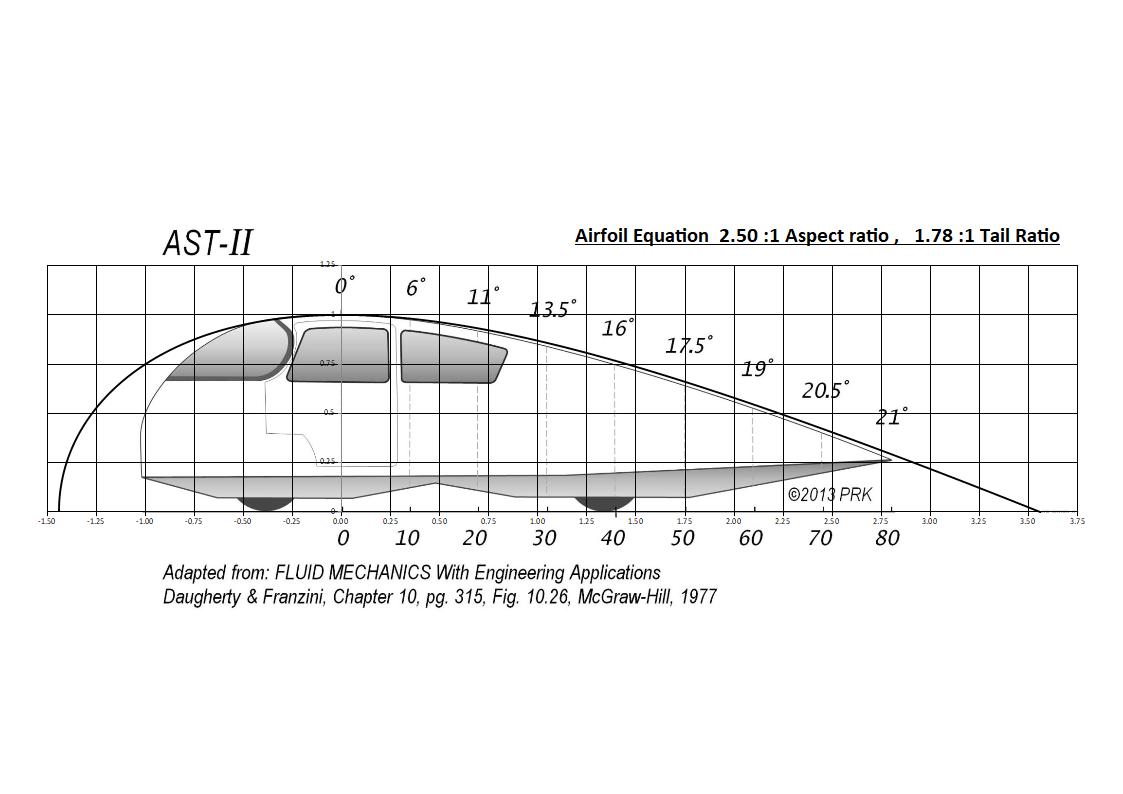
I tried as best I could to match up the key positions, firstly I was careful to only adjust template size by corners which maintains length:width integrity, then under high zoom lined up ground line of template with y=0 line on equation chart and then adjusted max height to y=1 on chart, then centered the template apex line 0% position with x = 0 line on chart, the top and bottom dash appear slightly displaced, so I went with the dashed line between the two which lined up best with the x=0 position.
I did do some overlays with stretching the two images and they lined up almost perfectly whether you stretched the template or compressed the chart, so at this stage it looks pretty good.

***Edit note - When I copied the high res ASII image it looked different under the curve, so zoom in and measure on screen and found the original ASII image was compressed, at 1.737:1 tail ratio and the High res one was stretched slightly at 1.787, so I compressed it a bit and did another one.

Corrected overlay below looks a bit better:



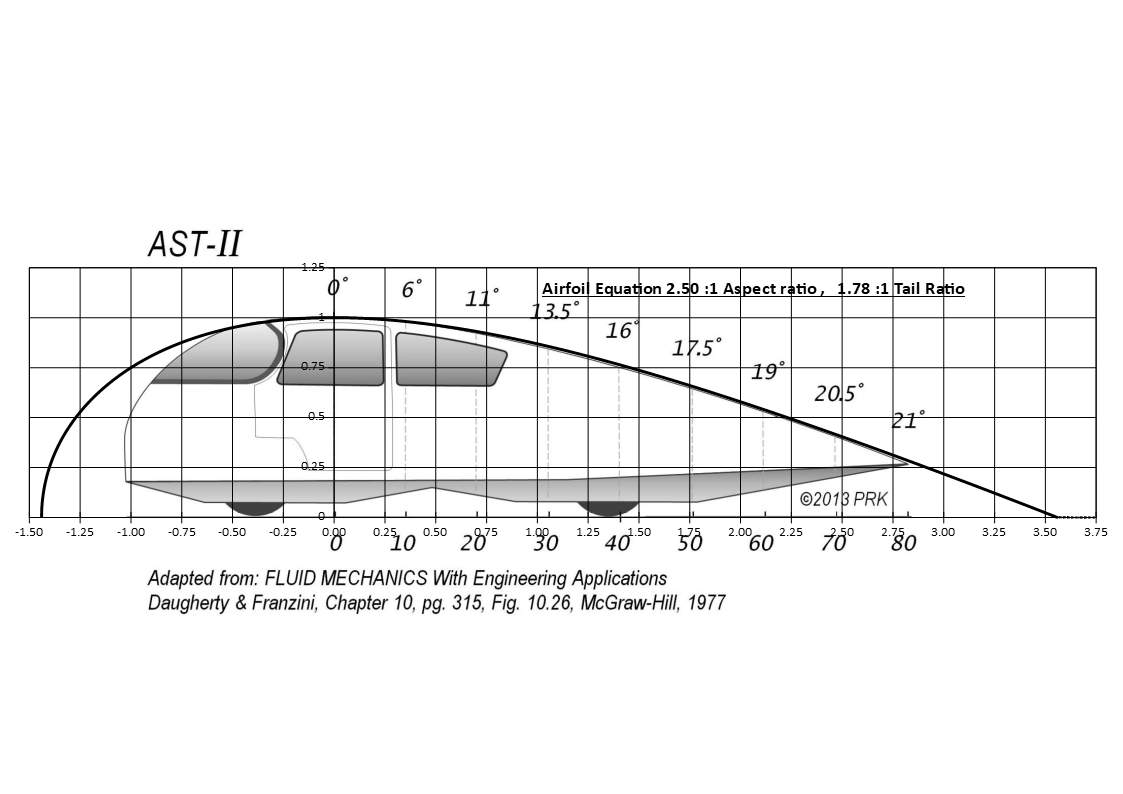
End of edit ***

The Data tables and Equation details are included below:



With the data table I've decided to go 5% increments so 20 data points, but to image the actual curve I used over 5,000 data points in the spread sheet, the table is just related to the tail portion, as this is what the majority is interested in. Column 2 & 3 are the data co-ordinates so where x=0 y=1 and at end where x=3.560 y=0, I set y-max at 1 so the data can easily be multiplied out by whatever your starting height is for the tail, eg if your starting height is 60 inches or 1.5 meters then multiply both x & y points by the either 60 or 1.5 and the result is in the units of your specific case.
The 4th and 5th columns just show the incremental fall and cumulative fall in the elevation points in the tail
The 6th and 7th columns are the angles of the equation tangent angles and the template tangent angles for a direct comparison, I have included the additional 10 points for the template in 5% increments, will explain later how I estimated those points.
The 8th and 9th columns compare the rate of change in the angles between the equation and template, the equation CoEfficients I used previously gave a kick back at the end of the tail, basically around the 80% mark the rate of change began to accelerate again, with this version I have pushed the change of rate to around y=0 or below, basically just beyond the end of the tail. The template points show that kick back rates at the end, but thats primarily because of the extra points I've inserted, the decision was a compromise by using a series of averaging factors to get the smoothest rate of change over time curve, what I've presented is the best option in my opinion.

For those really keen the equation is listed below the table, it basically gives you the y result for any x position, below that on the right hand side is the coefficient values I used, CoE 2,3,&4 went down to 9 decimal places as I was trying to get the equation balanced within the specified parameters, so in a number of places I have gone to 10 - 12 decimal places.

The other two details below the CoE values are the "tangent angle calculation factor", to calculate the tangent angle I used basic trigonometry, so calculating the angle of inclination between a point above and below the required tangent point, though this is not the true tangent at 10 decimal places the difference for this purpose is irrelevant. The other factor is "Added template segments factor", that's the added 5% incremental segments in between the specified template 10% increments, as mentioned I used the figure of 0.54, so just slightly weighted above average, just note this is only represented in the table template angle column and is not reflected anywhere in the inclinations of the images.

If you've gotten this far, you must be keen, the last left hand column is the airfoil and chart specs, the first 4 lines are the basic specs of the "body of revolution" and hence are self explanatory. The 5th line is the specified height, as said I chose 1 so that it makes up-scaling easy, the 6th line is a feedback line, it tells you this equation achieves a result of 1 with an accuracy to 10 decimal places.
The 7th & 8th line, simple 1.4400+3.5600=5.000, the 9th line 3.5600/2.000=1.7800, the 10th line 1.4400/5.0000=28.8% and finally the 11th&12th lines just specify the parameters of the chart so the curve fits within the frame.
That's me for now, over and out.

[aerohead]

Wow!
I'm happy to be reminded that I have zero computer chops,but others like yourself can easily navigate these waters.
Instant Grade-A+ work!
Thank you mucho! (past and present)

[ChazInMT]

Here's the High Res image I made of the template back when if you want a clean version.

Hi Res Link

[Tesla]

Thanks for that, just took a copy and will have a play later,
I just mirrored the chart to get an image for the full rotation



Anyone know how to produce a transparency?, I've made the chart transparent but every time I copy and save it in any format the page always ends up with a solid background.

Here is an overlay with the Bluefin Tuna.

[freebeard]

PNG and GIF have an alpha channel.That's what you want.

[Tesla]

Thanks, I'll see if I can work it out.

[California98Civic]

Clearly, the tuna could use some modding around the eyes and upper fin area. Get right on that, eh?

[Tesla]

With the Tuna maybe it's to allow for eating on the run, say when it opens mouth and flares gills, maybe God might sign in and explain if we're lucky.

*** Edit Note for post 711 at top of page, there appears to be a risk with distorting the proportions of the template or other images overlaid, even when you only use the corners to adjust size, there seems to be some distortions which begin to accumulate, so the dimensions of images need to be checked sometimes. Luckily the template has height and length markers and the 80% tail length:height ratio should be 1.78 x 80% = 1.424 ***

The Parametric Teardrop first appeared back on post 501 and elaborated more over the next page particularly with post 517 where the equation is explained more clearly and more comments and posts later in the thread.
I decided to have another look at that one too, if you look at the image from post 501, you see it's basically a distortion of a circular form.



As the CoEfficients are adjusted the equation pushes the bulge to one side until it pushes past the arc and then an S-curve is formed.

Edit Note **** The details below may not be quite right as I have discovered a minor error in the spread sheet that affects tail ratio, this may not be so bad as it may be another potential adjustment to the equation for fine tuning, I need to play with it more, will come back for a definitive edit in future****

With the constraints of the template form, 2.5:1 Aspect, 1.78:1 Tail ratio and the maximum allowable angle of 22% at any point means that for anything close to the template parameters, it can only be in the S-curve range. I thought there was an inherent limit with the parameters that tail ratio can only get to 1.77, but as I looked into it I found an error in the spread sheet, not in the base equation but with the offset & scaling to conform with template presentation. After playing with it for a while I finally came to what I thought was a pretty good compromise, the curve below:



The small curve is how the equation plots in standard form, then I had to add scaling and offset factors to present it in the template form, overlay below.



To get the best fit to template I went to Aspect ratio of 2.68 and tail at 1.91:1, sounds way out but when you look at the overlay you see the fore body is extended and the excess at rear is after the 80% mark, that's part of the effect of the S-curve. Its hard to see but there is a slight bulge between the 20-50% mark and the maximum angle was 19.5 degrees at around the 75% mark on template and then tapers back a bit.
I still need to layout the table better and put in columns to compare directly with template angles, so more to come later.

[Tesla]

I have re-done the equation with the specs from post 517 (3-Wheeler) just to explore those specs further, although it does come up with a 2.5:1 Aspect ratio, there are other issues which make it less than ideal.
I have made the x & y grid lines the same as the template so it's just a matter of lining up the height and length markers to compare, the overlay is below:



I think there's probably enough detail in the overlay to explain itself, particularly comparing the angles which start gentle but then accelerate to 27 degrees at the 80% mark, which breaks the 22 degree rule. Although the Aspect ratio is 2.5:1, the issue is that 1/3rd was in the fore body, which leaves the tail with a 1.67 tail ratio.

[Tesla]

When I started looking for an equation to match the template a few years ago, initially I just plotted the template angles in excel to try to match the curve, as I muddled about I found out that excel had a solver function which matches best fit equations to curves and I came up with this polynomial equation. I played with it for a while, but then got sidetracked with other ideas and it got left behind and forgotten, with this recent look into equations I dusted off the polynomial and had another look.
It just relates to the tail portion, but is much easier to manipulate and predict than the other 2, here is the overlay below:



It matches the template quite well, there's very little difference between the angles, the tail ratio comes out to 1.75 giving it a length of 3.49 as compared to 3.56 which is around 98% of specified length, although after this detailed study I do think an extension of the template drawing would come out a bit short of the 3.56 figure.
If you look hard you can see that the curve is just a fraction higher than template between 30-50%, but otherwise it's almost a perfect match.